PhD

Title The Landau-Lifshitz-Gilbert equation driven by Gaussian Noise

(French: L’équation de Landau-Lifshitz-Gilbert stochastique avec bruit gaussien)

Director De Bouard, Anne, Research Director at CNRS
Co-director Alouges, François, Professor at École Polytechnique, Palaiseau, France
Phd awarded by École Doctorale n° 447: Sciences et Technologies.
Place of exercise Centre de Mathématiques Appliquées (CMAP), Polytechnique ParisTech. UMR CNRS 7641, Route de Saclay, 91128 Palaiseau, France.
Speciality Applied Mathematics.
Type of scholarship ASN (contrat flèché normalien).

The manuscript of the thesis is available online at the following url:
https://pastel.archives-ouvertes.fr/tel-01265433v1/document .

The thesis was presented and publicly defended by Antoine Hocquet on December 7, 2015 in front of the jury composed of

M. Beniamin Goldys Professor, University of Sydney, Reporter
M. Massimiliano Gubinelli Professor, Université Paris Dauphine, Reporter
M. Andreas Prohl Professor, Universität Tübingen, Reporter
M. Olivier Goubet, Professor, Université de Picardie Jules Verne, Examinator
M. Lorenzo Zambotti Professor, Université Pierre et Marie curie, Examinator
M. François Alouges Professeur, École Polytechnique, co-Director
Mme Anne de Bouard Senior researcher at CNRS, Director

Summary

The main goal of the thesis is to study the influence of a Gaussian noise in the Stochastic Landau-Lifshitz-Gilbert equation.

The latter is a stochastic PDE of unknown u=u (t,x), verifying a geometric constraint on the modulus of solutions, and written as the following evolution equation in the space L^2 =L^2(O;R^3) (where O is some bounded region of R^d, d=2,3):

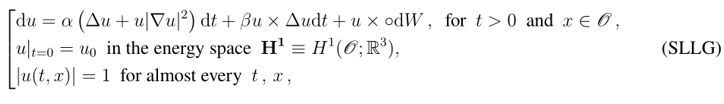
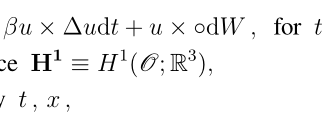
(Stratonovitch sense), where W is a Wiener process in L^2, whose covariance is trace-class in H^1, and alpha >0 is the damping constant, while beta (real number) is the gyromagnetic ratio.

Here the cross product notation denotes the usual vector product in R^3.

Chapter 1 is devoted to local solvability. We propose a mild formulation and prove existence and uniqueness with zero magnetic ratio.

A specific study of 2D is made in the following three chapters. A strong, global solution (probabilistic sense) is obtained in Chapter 2, using a compactness method.

Chapter 3 focuses on uniqueness. A famous result obtained in the 80's by A. Freire and M. Struwe was providing uniqueness for the deterministic equation by supposing the energy non-increasing w.r.t. time, an assumption that becomes impossible in the noisy case. We show the uniqueness of the solutions whose energy verifies a certain (super)-martingale property.

Chapter 4 gives the existence of solutions exploding in finite time (when beta is 0): a singularity appears with positive probability, no matter how the initial data is chosen.

Returning then to the general case d<= 3 and real (non-zero) beta, we introduce in chapter 5 a new numerical scheme and show its convergence in law. This scheme is semi-discretized in time and preserves the constraint on the modulus of solutions.

The corresponding algorithm is then implemented in Chapter 6 using finite elements. We give a practical method to approach a regular noise in space, and we numerically test the stability of the blow-up phenomenon.

Keywords
Landau–Lifshitz equation · Numerical analysis · Stochastic partial differential equations · Harmonic Maps · Blow-up

Mathematics Subject Classification

35K55 · 60H15 · 65Z05 · 33C10 · 35B44